♪ 悲しいよね 甘えさせて 赦しすぎて 自分を亡くすよ ♪

ネタもと：僕は優しくありませんょ?

咲子さん：申し訳なし（「先越された」を変換したら、「咲子された」になった）

オセロだそうです。おもしろそう。え？タイマー祭り開催中？？？あ、、、いや、こっちもおもしろそうだし、コード書いちゃったし。。。

というわけで、オセロなの！漫才師じゃないよ。

あ、「オセロ」って、どこかの登録商標だった。「リバーシ」です。

注意：ここに出すコードは、動くものではありません。コンパイルすらしていません。考え方を参考にしてください。

リバーシです。波瀾万丈盤上に白と黒の駒を置いて、同じ色の駒で、違う色の駒を挟み、ひっくり返します。

強さを無視するとして、「置ける場所」を考えるルーチンを考えてみます。

まず、リバーシの盤に注目します。盤には、駒を置けるマスがあります。このマスには、「何もない」「白い駒が置いてある」「黒い駒が置いてある」という状態があります。まず、この“状態”を「コード化」します。

コード化するのですが、もう一つ考えておきます。「盤の外」という状態です。指定した位置が「盤の中に収まっているか」をチェックする箇所を少なくするため、「盤の外」という「状態」を用意します。「この位置の状態はどうなっていますか？」と聞かれたときに、「盤の外です」という答え方ができます。

// マスの状態をコードで表す
enum マスの状態 {
    外 = 0
    , 空
    , 白
    , 黒
};

次に、「このマスの状態は、どうなっていますか？」と尋ねられたときに、「こうなっています」と返すところ。位置を指定して尋ねると、その位置の状態が返ってきます。なんか、元ネタでは「６×６で」となっているので、マスの数は変更できるようにしておきます。

// マスの状態を返す
private const System.Drawing.Size 盤の大きさ = new Size(8, 8); // って、できたっけ？
private マスの状態[][] マス; // どこかで初期化する
public マスの状態 マスの状態を返す(System.Drawing.Point 位置) {
    if (位置.X < 0 || 位置.X >= 盤の大きさ.X || 位置.Y < 0 || 位置.Y >= 盤の大きさ.Y) {
        return マスの状態.外; // はみ出とうやん
    }
    return マス[位置.X][位置.Y];
}

次に、「このマスは、ひっくり返すことができますか？」と尋ねられたときに、「はい」または「いいえ」を返すところ。

// 位置と色を指定して、その色にひっくり返すことができるかどうかを返す
public bool ひっくり返せますか？(Point 位置, マスの状態 この色にする) {
    if (この色にする == マスの状態.外 || この色にする == マスの状態.空) {
        return false; // 色じゃないからね
    }
    マスの状態 状態 = マスの状態を返す(位置);
    if (状態 == マスの状態.外 || 状態 == マスの状態.空) {
        return false; // ひっくり返すものがないからね
    }
    if (状態 == この色にする) {
        return false; // 同じ色だからね
    }
    return true;
}

これで、盤のどこかを指定して、「どうなっているのか？」、「色をひっくり返すことができるのか？」を調べることができるようになりました。

じゃぁ、次。「ここに、この色の駒を置くことができますか？」と聞いて、「はい」または「いいえ」を返すところ。

物事は、順番に考えます。「ここに、この色の駒を置くことができますか？」というのは、いくつかの条件をクリアして初めて返答ができます。の条件とはなんでしょう？一つは、「盤の内側であること」です。当たり前ですね。でも、その当たり前を忘れてしまいがちです。あるいは、当たり前だからチェックしないでいます。それがオーバーフローの脆弱性につながります。なので、必ずチェックします。

// 位置と色を指定して、駒を置けるかどうかを返す（未完）
public bool 駒を置けますか？(Point 位置, マスの状態 この色の駒) {
    if (この色の駒 == マスの状態.外 || この色の駒 == マスの状態.空) {
        return false; // 色じゃないからね
    }
    マスの状態 状態 = マスの状態を返す(位置);
    if (状態 == マスの状態.外) {
        return false; // 盤外には置けません
    }
    return true; // 暫定
}

次の条件。「他の駒が置いてあるところには置けない」です。当たり前ですね。当たり前なので、必ずチェックします。

コードの前に。「盤外ではなく、他の色の駒がない」というのは、どういう状態でしょう？つまり、「マスの状態.空」の時だけ置ける、ということですね。

// 位置と色を指定して、駒を置けるかどうかを返す（未完）
public bool 駒を置けますか？(Point 位置, マスの状態 この色の駒) {
    if (この色の駒 == マスの状態.外 || この色の駒 == マスの状態.空) {
        return false; // 色じゃないからね
    }
    マスの状態 状態 = マスの状態を返す(位置);
    if (状態 != マスの状態.空) { // この行が変わりました
        return false; // 空でないところには置けません
    }
    return true; // 暫定
}

いよいよ本題。「ここに置くことで、ひっくり返すことができる駒があるか」というところ。

まず、「ひっくり返す」とは、どういう事でしょうか。あるところを起点に、「一直線に他の色が置いてあり、最後に置こうとしている駒と同じ色があること」、ですね。こういうのは絵を描くと、とってもわかりやすくなります。

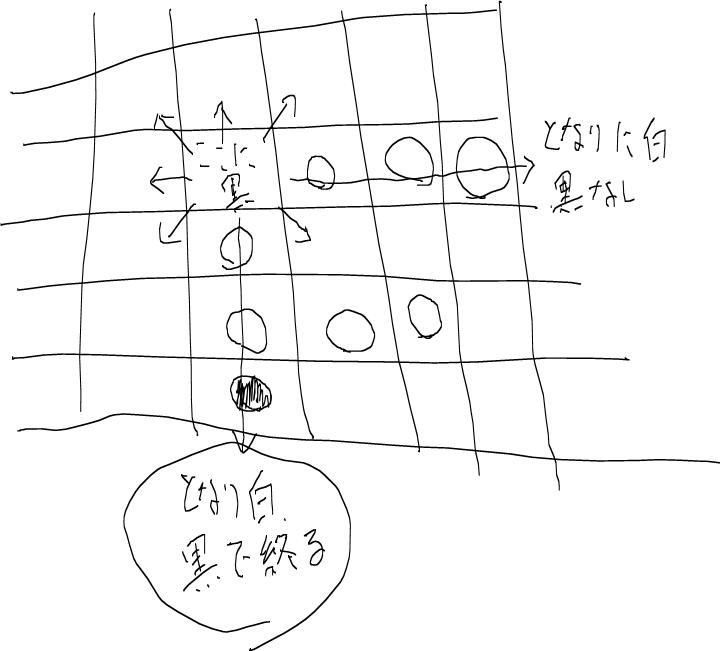
で、こういう探索を8方向に対して行い、結果的に1つ以上のひっくり返せる駒があれば、そこに置ける、となります。

で、8方向とはどういう事か、を考えます。こんなものは、総当たりして法則を探せばいいのです。

起点を (5, 5) とします。まず、上。(5, 4), (5, 3), (5, 2), (5, 1), (5, 0) です。以下、面倒なので省略。つまり、上は「y が 1 ずつ減る」、右上は「x が 1 ずつ増え、y が 1 ずつ減る」、右は「x が 1 ずつ増える」、、、ちょ～～～っと待った。

ここで、「増える」「減る」と、“言葉”が違うものが現れました。これは、プログラムする上では、難しくしてしまいます。プログラムは、同じ言葉を並べるように考えると、繰り返しが使えるようになり、短く書くことができるようになります。

また、上の時は「y が 1 ずつ減る」で、右の時は「x が 1 ずつ増える」です。x, y が、出てくるときと出てこないときがあります。こういうものは分岐構文で表すのですが、分岐が増えるほど、プログラムを難しくしてしまいます。

この2つを、数字が変わるだけで同じ言葉になるように考えるのが、プログラムを考える、ということなのかもしれません。

では、どうしましょうね。こうします。

上は「x が 0 ずつ増える。y が -1 ずつ増える。」右上は「x が 1 ずつ増える。y が -1 ずつ増える。」右は「x が 1 ずつ増える。y が 0 ずつ増える。」右下は「x が 1 ずつ増える。y が 1 ずつ増える。」下は「x が 0 ずつ増える。y が 1 ずつ増える。」左下は「x が -1 ずつ増える。y が 1 ずつ増える。」左は「x が -1 ずつ増える。y が 0 ずつ増える。」左上は「x が -1 ずつ増える。y が -1 ずつ増える。」。。。となります。これで、増える数が -1, 0, 1 と変化するだけで、他の言葉は同じになりました。

すなわち、上から右回りに、(0, -1), (1, -1), (1, 0), (1, 1), (0, 1), (-1, 1), (-1, 0), (-1, -1) の増分値で変化する座標を調べれば、それぞれの方向へ一直線に検査することができます。

// 位置と色を指定して、駒を置けるかどうかを返す（未完）
static private Size[] 増分リスト = {
    new Size(0, -1)
    , new Size(1, -1)
    , new Size(1, 0)
    , new Size(1, 1)
    , new Size(0, 1)
    , new Size(-1, 1)
    , new Size(-1, 0)
    , new Size(-1, -1)
};
public bool 駒を置けますか？(Point 位置, マスの状態 この色の駒) {
    if (この色の駒 == マスの状態.外 || この色の駒 == マスの状態.空) {
        return false; // 色じゃないからね
    }
    マスの状態 状態 = マスの状態を返す(位置);
    if (状態 != マスの状態.空) {
        return false; // 空でないところには置けません
    }
    ArrayList 返せる駒リスト = new ArrayList(32);
    foreach (Size 増分 in 増分リスト) {
        // 次はここを考える
    }
    return (返せる駒リスト.Count > 0);
}

では次に、「一直線に、ひっくり返せるかどうかを調べる」ところです。上のリストで、「// 次はここを考える」としている箇所です。

ここは、これから駒を置こうとしている場所を考えるとやっかいなので、置こうとしている場所の周囲だけを考えます。先ほど、「ひっくり返せますか？」メソッドを作りました。このメソッドは、ひっくり返せるなら true を返します。false、つまりひっくり返せないときは、どんなときでしょうか。駒が置かれていないとき、盤外の時、同じ色の駒の時です。したがって、「ひっくり返せますか？」メソッドが true を返す間、増分を足し込んで検査する座標を変化させていけばよいようです。

ちょっと待ってね。まだ、コード化するのは早いですよ。机上で検証できるものは、机上で検証してしまいます。というのも、検証が中途半端だと、「これで動くはずだ」と思いこんでしまうからです。この思いこみは、デバッグの大敵です。

さて、ひっくり返せますか？メソッドが true を返せば、返せる駒リストに、その検査した座標を格納していくことにします。そうすると、隣が同じ色の駒だったり、空、あるいは盤外だった場合は、リストに何も入らないからです。これによって、返せる駒リストが 0 かどうかで、その位置に置けるかどうかが決まりそうです。

本当にそうですか？

ひっくり返せますか？メソッドを、よく見てください。このメソッドが返す本当の値は、「違う色の駒である」という事です。つまり、本当にひっくり返すためには、まだ他の判断が要ります。つまり、「同じ色の駒で挟まれていること」を調べなければなりません。どうやって？簡単ですね。false が返ってきた位置の駒が、置こうとしている駒の色と同じかどうかを調べればいいわけです。マスの状態が同じ色であれば、今リストに入っているものをひっくり返すことができます。

// 位置と色を指定して、駒を置けるかどうかを返す（未完）
static private Size[] 増分リスト = {
    new Size(0, -1)
    , new Size(1, -1)
    , new Size(1, 0)
    , new Size(1, 1)
    , new Size(0, 1)
    , new Size(-1, 1)
    , new Size(-1, 0)
    , new Size(-1, -1)
};
public bool 駒を置けますか？(Point 位置, マスの状態 この色の駒) {
    if (この色の駒 == マスの状態.外 || この色の駒 == マスの状態.空) {
        return false; // 色じゃないからね
    }
    マスの状態 状態 = マスの状態を返す(位置);
    if (状態 != マスの状態.空) {
        return false; // 空でないところには置けません
    }
    ArrayList 返せる駒リスト = new ArrayList(30);
    foreach (Size 増分 in 増分リスト) {
        Point 検査座標 = Point.Add(位置, 増分);
        ArrayList 違う色の駒リスト = new ArrayList();
        while (ひっくり返せますか？(検査座標, この色の駒) == true) {
            違う色の駒リスト.Add(検査座標);
            検査座標 = Point.Add(検査座標, 増分);
        }
        if (マスの状態を返す(検査座標) == この色の駒) {
            返せる駒リスト.AddRange(違う色の駒リスト);
        }
    }
    return (返せる駒リスト.Count > 0);
}

はい、これで終わり...じゃないです。

今作ったものは、ひっくり返す駒のリストを作りながら、それを捨ててしまっています。つまり、ここに置けるという判断をして、そこに駒を置いた後、またひっくり返す駒を調べなければなりません。これは、効率がよいとは言えないでしょう。

そこで、こうしましょう。そこに置いたときに、ひっくり返すことができる駒のリストを返すメソッドを提供する。このメソッドの戻り値が、空リストでなければ置くことができる、と。

ということで、ちょっと手直し。

// 位置と色を指定して、ひっくり返すことができる駒のリストを返す
static private Size[] 増分リスト = {
    new Size(0, -1)
    , new Size(1, -1)
    , new Size(1, 0)
    , new Size(1, 1)
    , new Size(0, 1)
    , new Size(-1, 1)
    , new Size(-1, 0)
    , new Size(-1, -1)
};
public ArrayList ひっくり返せる駒のリストを返す(Point 位置, マスの状態 この色の駒) {
    if (この色の駒 == マスの状態.外 || この色の駒 == マスの状態.空) {
        throw new ArgumentException("おいおい");
    }
    ArrayList 返せる駒リスト = new ArrayList(30);
    if (マスの状態を返す(位置) != マスの状態.空) {
        return 返せる駒リスト;
    }
    foreach (Size 増分 in 増分リスト) {
        Point 検査座標 = Point.Add(位置, 増分);
        ArrayList 違う色の駒リスト = new ArrayList();
        while (ひっくり返せますか？(検査座標, この色の駒) == true) {
            違う色の駒リスト.Add(検査座標);
            検査座標 = Point.Add(検査座標, 増分);
        }
        if (マスの状態を返す(検査座標) == この色の駒) {
            返せる駒リスト.AddRange(違う色の駒リスト);
        }
    }
    return 返せる駒リスト;
}

「ひっくり返せる駒のリスト」じゃなく、「ひっくり返せるマスのリスト」じゃないか！という突っ込みは、ご容赦を。つか、それぞれの名前は、深く考えてないし...